
Bienvenue sur ma page web qui va vous permettre, oui vous, heureux terminalien S que vous êtes, de consulter en ligne tout le programme en obligatoire de TS que j'ai élaboré durant l'été 2000... Vous allez ainsi pouvoir en un clin d'oeil revoir les propriétés essentielles des complexes, intégrales, exponentiellles, probabilités... bref, une mini bible de TS...
PROGRAMME ABORDE :
| Analyse |
- Fonctions numériques
: étude locale et globale : - Calcul intégral
: |
| Algèbre, géométrie |
- Equations,
Système d'équations linéaires : - Nombres complexes
: - Calcul vectoriel
et géométrie : |
| Combinatoire, probabilités |
- Combinatoire,
dénombrements : - Probabilités
: |
Vous trouverez
ci-dessous un extrait de mon résumé, pour vous en donner un
aperçu... Cependant, gardez bien à l'esprit que j'ai profondément
remanié cet extrait par rapport à l'original pour avoir un affichage
correct. Les versions téléchargeables sont bien plus lisibles
et agréables...
Enfin, vous avez à votre disposition, à la fin de cette page,
le dit résumé à télécharger, et ce sous
deux formats : en fichier .doc (donc erreur de compatibilité avec votre
logiciel assurée à 98.256%), ou en fichier .pdf, lisible avec
le logiciel gratuit Adobe Acrobat Reader (si vous ne l'avez pas, un lien vous
permettra de le télécharger). Remarquons que si vous avez déjà
ce logiciel, le résumé en .pdf s'affichera directement sur cette
fenêtre...
Erreur dans le résumé ? Exercice que vous n'arrivez pas à
résoudre ? Un point du programme vous reste obscur ? Dîtes-le
dans mon forum
! J'y répondrai au plus vite...
ANALYSE — CHAPITRE 1
I_ Fonctions numériques globales et locales.
A_ énoncé sur les limites.
Les limites données dans ce paragraphe sont pour la plupart issues de théorèmes de comparaison sur les fonctions, c'est-à-dire que connaissant une relation de comparaison entre celles-ci, que ce soit en + ou - infini, ainsi que la limite de l'une d'entre elles, si les hypothèses sont vérifiées, on peut en déduire la limite de l'autre.
Propriété
: soit A réel, f et u deux fonctions à valeurs dans l'ensemble des
réels.
Si, pour tout x > A, f(x)>u(x) et lim u(x) = + infini alors lim f(x)
= + infini.
On peut donner l'équivalent de cet énoncé dans le cas d'une limite en - infini :
Propriété
: soit A réel, f et u deux fonctions à valeurs dans l'ensemble des
réels.
Si, pour tout x > A, f(x)<u(x) et lim u(x) = - infini alors lim f(x)
= - infini.
Nous pouvons de même donner ces propriétés lorsque x tend vers - infini...
Graphiquement,
on pourrait traduire ces propriétés par :
— dans le premier cas -> la courbe représentative de f est
au dessus de celle de u, qui tend vers + infini ;
— dans le second cas -> la courbe représentative de f est en
dessous de celle de u, qui tend vers - infini.
Il est également possible de donner ces propriétés dans le cas de limites finies :
Propriété
: soient f et u deux fonctions à valeurs dans l'ensemble des réels,
A et L deux réels.
Si, pour tout x > A, |f(x)-L| < u(x), et lim u(x) = 0, alors lim f(x)
= L.
Les hypothèses de cette propriété signifient en faît que l'écart entre la fonction f et le réel L diminue au fur et à mesure que x augmente, jusuq'à ce que cet écart s'annule (u(x) tend vers 0). Ainsi, le fonction f se rapproche infiniment du réel L : lim f(x) = L.
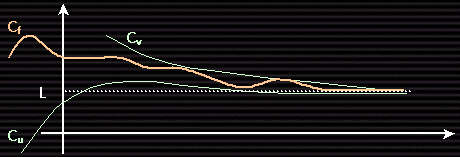
Nous pouvons à présent donner le théorème des gendarmes :
Théorème
: soient f, u et v trois fonctions à valeurs dans l'ensemble des réels,
A et L deux réels.
Si pour tout x > A, u(x) < f(x) < v(x) et lim u(x) = lim v(x) = L,
alors lim f(x) = L.
Ce théorème est également appelé "théorème d'encadrement". En effet, on encadre une fonction f par deux fonctions u et v qui tendent vers la même limite en + infini.
La propriété suivante n'a pas une très grande utilité pour la résolution d'exercices ou de problèmes. Cependant, elle contient une subtilité qui mérite réflexion. Par conséquent, elle peut constituer pour le jury une question idéale pour tester votre pertinence et votre compréhension…
Propriété
: soient f et g deux fonctions à valeurs dans l'ensemble des réels,
A, L et L' trois réels.
Si, pour tout x >A, f(x) inférieur ou égal à g(x),
lim f(x) = L et lim g(x) = L', alors L inférieur ou égal à
L'.
La
subtilité évoquée réside dans le faît que
la propriété reste vraie si on remplace f(x) inférieur
ou égal à g(x) par une inégalité stricte : f(x)
< g(x), mais elle devient fausse si on ajoute à cette transformation
: L < L'.
En effet, lorsque l'on passe aux limtes, les inégalités deviennent
toujours larges !
Exemple
: soit f : x —> 1-(1/2x), et g —> 1+(1/2x).
Pour tout x > 0, on a f(x) < g(x). De plus, avec les notations de la
propriété, L=1 et L'=1, d'où L=L' !
Enfin, il reste le cas des limites pour une composition de fonction :
Théorème
: soient a, b et c trois éléments pouvant soit être des
réels, soit valoir + ou - infini, f et g deux fonctions à valeurs
dans l'ensemble des réels et pouvant avoir des limites infinies, avec
f définie au voisinage de a et g définie au voisinage de b.
Si f(x) tend vers b quand x tend vers a, et si g(x) tend vers c quand x tend
vers b, alors (g°f)(x)=g[f(x)] tend vers c quand x tend vers a.
Ce résultat est donc une composition de fonctions dans le cas d'une limite.
Les propriétés et théorèmes précédents se retrouvent aisément par une simple visualisation dans un cas simple (ne pas hésiter à faire un petit dessin au brouillon !). Les limites exposées ici servent essentiellement dans les problèmes, aussi il est absolument nécessaire de les connaître et surtout de savoir les appliquer sans aucune hésitation !
B_ calcul différentiel.
Dans ce paragraphe, nous nous intéressons à tout ce qui concerne dérivée et primitive de fonctions usuelles et de fonctions composées, ainsi qu'aux accroissements finis. Cependant, certaines fonctions (comme l'exponentielle) seront définies plus tard : reportez vous à la partie correspondante...
( à suivre...)
Voici
donc la fin de cet extrait... J'espère qu'il vous a plu ! La version
complète est téléchargeable ci-dessous. Je précise
une fois encore qu'il est extrèmement recommandé de télécharger
la version au format "pdf" car il est compatible sur n'importe quel
ordinateur et lisible avec ADOBE ACROBAT READER que vous avez déjà
probablement installé. Si ce n'est pas le cas, cliquez sur l'image
en dessous du tableau.
Remarquons également que si vous cliquez sur la version ".pdf"
non zippée, le résumé apparaîtra directement dans
cette fenêtre (toujours si vous avez acrobat reader...). Vous aurez
alors toujours la possibilité de le sauvegardez sur votre propre ordinateur
(c'est une fonctionnalité de acrobat reader)...
Enfin, n'hésitez pas à me contacter au sujet de ce résumé
(ou autre chose d'ailleurs), si vous auriez souhaité plus de détails
par exemple... N'hésitez pas non plus à le distribuer autour
de vous !
|
Taille
: 331 Ko
|
|
|
Taille
: 537 Ko
|
|
|
Taille
: 489 Ko
|
Accès à la page de référencement des sites