Vous vous demandez comment se forme un arc-en-ciel ? Pourquoi celui-ci a une telle forme ? Pourquoi il y a toutes ces couleurs ? Cette page est faîte pour vous ! En effet, l’arc-en-ciel est sans aucun doute le phénomène atmosphérique le plus populaire, car le plus facile à voir. On l’observe lorsqu’il pleut, et que le soleil est visible. Nous allons ainsi étudier la physique associée à l’arc-en-ciel. Certains passages vous paraîteront peut-être obscurs ou pas assez détaillés, donc n’oubliez que je peut répondre à vos questions par mail (enfin, si j’y parviens)!
Dans tout le raisonnement qui va suivre, nous considèrerons les gouttes d’eau comme étant de forme sphérique, et nous supposerons le soleil à l’infini.
REMARQUE IMPORTANTE : De nombreux bugs vont probablement apparaître (veuillez m’en excuser, et encore merci microsoft !). Aussi, je vous propose la même version téléchargeable (sans aucun bug) à la fin.
I. Les étapes de formation.
a) Bref rappel des lois fondamentales de l’optique.
L’arc-en-ciel est en fait la conséquence de deux phénomènes principaux qui ont été mis en équation par Descartes pour l’un, et par Cauchy pour l’autre.
· Deuxième loi de Snell-Descartes -> La réfraction.
-> La réflexion totale.
Cette loi s’applique à un rayon lumineux qui traverse un dioptre séparant deux milieux plus ou moins réfringents, c’est à dire deux milieux dont la « transparence » (que l’on caractérise par les indices de réfraction ) est différente. Enonçons cette loi :
| n1 . sin(i1) = n2 . sin(i2) | |
Nous pouvons remarquer expérimentalement que lorsqu'un rayon lumineux passe d'un milieu réfringent à un milieu moins réfringent, plus l'angle d'incidence augmente, et plus le rayon émergent se rapproche du dioptre. Il existe donc un angle critique noté qc tel que lorsque l'angle d’incidence est égal à cette valeur, le rayon réfracté est de 90° . qc se déduit de la deuxième loi de Snell-Descartes citée auparavant.
En effet, cette loi n’est valable qu’à une certaine condition qui doit être respectée : dans le cadre de notre étude, n1=n[air]=1 et n2=n[eau]=1.333 .En notant q l’angle incident, étant donné que la fonction sinus est à valeur dans [-1,1], cette équation est applicable si et seulement si :
q = Arcsin (n2/n1)
On note donc l'angle critique :
qc=Arcsin(n[air]/n[eau])
Dès que l'angle d'incidence dépasse l'angle critique, il sera entièrement réfléchi dans le milieu le plus réfringent. On a alors réflexion totale.
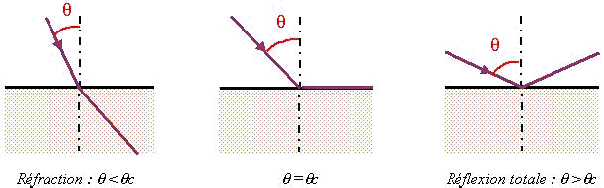
Attention !
Sur ces trois cas de figures, l’indice de réfraction du milieu orange est inférieur à l’autre.
· Loi de Cauchy.
La lumière blanche du soleil comprend toutes les radiations (longueurs d’onde) comprises entre 400 nm (violet) et 800 nm (rouge). En notant l la longueur d’onde d’un rayon, nous pouvons rappeler la loi de Cauchy :
n0 et c sont des
constantes positives qui dépendent de la longueur d’onde choisie.
n
= n0 +
Par conséquent, pour un même milieu, l’indice de réfraction varie sensiblement selon la longueur d’onde : chaque couleur, ayant sa propre longueur d’onde, est ainsi réfractée différemment (puisque n est d’autant plus grand que l est petit). On observe alors une dispersion du faisceau incident ( l’onde initialement polychromatique se divise en rayons monochromatiques ).
|
 |
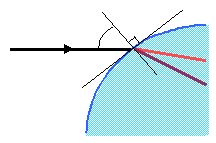b) Les étapes de formation de l’arc-en-ciel.
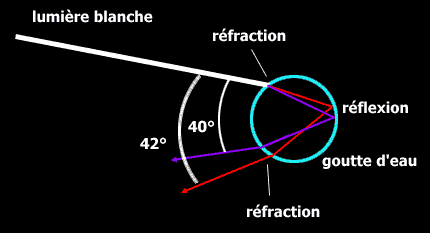
Passage d’un rayon provenant du soleil dans une goutte.
Attachons-nous dans cette partie à l’étude de la formation de l’arc-en-ciel primaire (le plus visible). Cette formation se fait en cinq étapes, qui sont les suivantes :
->une première réfraction :
Le rayon du soleil frappe une goutte d'eau, entrant alors dans un milieu dont l'indice de réfraction est différent. On a donc déviation de ce rayon.
->une première dispersion :
En effet, la lumière blanche du soleil comprenant toutes les longueurs d’onde visibles par l’homme (400 à 800 nm.), il y a donc décomposition de ce rayon polychromatique en ses composantes monochromatiques (séparation des couleurs). Cette décomposition a été paramétré par la loi de Cauchy.
->une réflexion totale interne :
L’indice de l’eau est supérieur à celui de l’air, et quelques rayons frappent le fond de la goutte avec une incidence supérieure à l'angle critique (voir la suite pour le calcul de cet angle). On a donc une réflexion totale interne dans la goutte pour quelques rayons.
->une seconde réfraction ;
Les rayons rencontrent une nouvelle fois l’interface « eau-air ».
->une seconde dispersion.
La première dispersion est accentuée, dûe à la seconde réfraction.
II. Etude de la déviation.
a) Par rapport à l’angle d’incidence.
Afin d’avoir un cas idéal, on modélise les gouttes d’eau comme étant de forme sphérique. On s’attache donc au parcours d’un rayon monochromatique, nous évitant ainsi l’étude supplémentaire de la dispersion.
 |
|
|
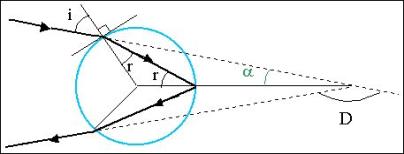L'expression littérale de la déviation s'écrit, en degrés :
D=180-2.a
D=180-2.[180-i-(180-2r)] soit :
D=180+2.i-4.r
Exprimons une relation donnant l’angle émergent r en fonction de l’angle d’incidence i et de l’indice de réfraction de l’eau, noté n :
Par la loi de Snell-Descartes, 1.sin(i)=n.sin(r), d'où :
r=arcsin(sin(i)/n)
De plus, par dérivation, on obtient:
di.cos(i)=n.dr.cos(r), soit dr=
On calcule donc la dérivée de la déviation par rapport à l'angle d'incidence :
D=180+2i-4r
dD=2di-2. 
d'où :
= 2.(1-2.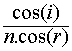 
)
Par des considérations de symétrie, on étudie D(i) sur l’intervalle [0°;90°].
La déviation passe donc par un extremum (qui se révèle être un minimum) pour un certain angle d’incidence, que l’on note im. Cet angle est tel que :
1-2.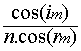 
=0 soit 2.cos(im)=n.cos(rm)
|
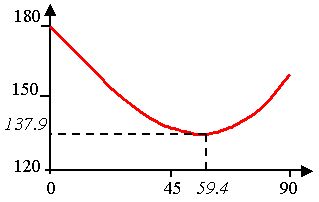
Sur ce graphe, toutes les valeurs
sont données en degrés.n
a été fixé à 1.33 et
im vaut alors environ 59.4° . Du faît de l’extremum, la déviation
reste sensiblement la même au voisinage de im. angle(i)
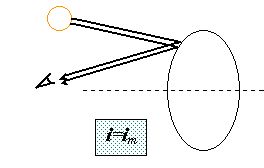
Ainsi, pour un angle d’incidence d’un rayon rentrant dans une goutte d’eau proche de im, nous aurons accumulation des rayons réfractés dans une seule direction, donc plus d’énergie, d’où une visibilité accrue du phénomène. A contrario, pour i¹im , les rayons réfractés seront plus dispersés et, par conséquent, auront une puissance plus faible, comme le montre l’illustration suivante :
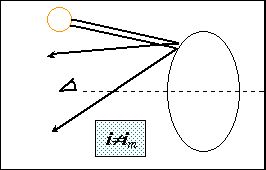
Expérience :
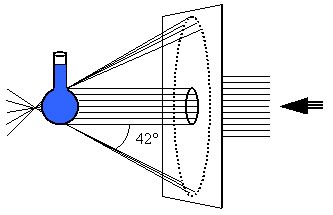
Comme modèle d’arc-en-ciel, on peut réaliser l’expérience du ballon d’eau qu’on éclaire avec un faisceau grossièrement parallèle de lumière blanche. C’est à partir de cette expérience que Freiberg puis Descartes ont établi une théorie de l’arc-en-ciel.
En utilisant un
faisceau large couvrant toute la sphère, on observe le spectre
primaire circulaire sur l’axe du faisceau, ainsi qu’un spectre
secondaire (non explicité ci-contre).
A présent, passons au calcul de l’angle de déviation des rayons en tenant compte de leurs longueurs d’onde respectives, engendrant des différences vis à vis de l’indice de réfraction pour l’eau.
Remarquons que l’indice de l’air varie également, mais cela a déjà été pris en compte lors du calcul de la déviation effectué précédemment (début du paragraphe).
b) Par rapport à l’indice de réfraction.
Calculons im en fonction de n :
im est tel que : 2.cos(im)=n.cos(rm)
Or, rm=Arcsin(sin(im)/n) (voir plus haut), d’où :
2.cos(im)=n.cos(rm)
=n.cos[arcsin(sin(im)/n)]
=n.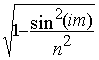 
Si on élève l’équation ci-dessus au carré, on obtient :
4.(1-sin2(im))=n2(1-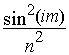 
) 
4-4.sin2(im)=n2-sin2(im)
sin2(im)= 
im=arcsin(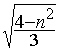 
)
Finalement,
on obtient : im=arcsin(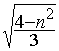 
)
Récapitulons donc les équations reliant toutes les données du phénomène :
1. Déviation en fonction de l’angle d’incidence et de l’indice de réfraction de l’eau :
D(i)=180+2.i-4.Arcsin(sin(i)/n)
2. Angle d’incidence minimal en fonction de l’indice de réfraction :
im=
arcsin(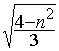 
)
On peut donc tirer de ces équations l’angle de déviation minimal uniquement en fonction de l’indice de réfraction :
Dm(n)=180+2.arcsin( 
)-4.arcsin{sin[arcsin( 
)]/n}
Dm(n)=180+2.arcsin(
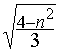)-4.arcsin(
)
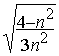Jusqu’à présent, nous avons toujours pris l’indice de l’eau égal à 1.333 .On obtient alors un angle de déviation égal approximativement à 138° :
im = 59.4° ; rm =40.3° ; Dm = 137.9°
Nous venons de calculer la déviation minimale entre le rayon "initial" et le rayon "final" suivant les notations que l’on a adoptées précédemment.Or, il ne faut pas oublier que l’indice de réfraction de l’eau varie en fonction de la longueur d’onde du rayon ! Par conséquent, en supposant que le soleil n’émette que ce type de rayon monochromatique, on a la situation suivante :
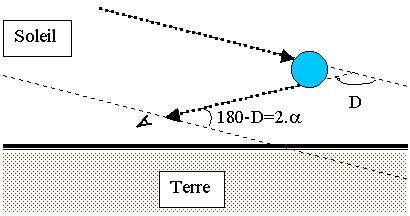
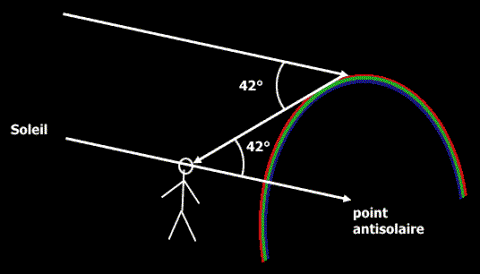
Dans notre cas de figure, nous observerons donc un arc de cercle d’une seule couleur si le soleil éclaire des gouttes de pluie, et que ces gouttes sont situées de telles manières que l’angle entre le soleil, les gouttes et nos yeux soit de 180-138°, soit 42°, dans la configuration illustrée ci-dessus . On retrouve alors les valeurs données dans les schémas précédents.
On en conclut donc que les arcs-en-ciel sont en réalité…circulaires !!! Ils réalisent en faît un cône dont nos yeux sont le sommet, et d’axe le rayon provenant du soleil et passant par nos yeux. En effet, toutes les génératrices constituant ce cône font un angle de 42° par rapport à l’axe central même si, évidemment, on ne voit le cône que partiellement, du faît qu’il ne pleut pas et qu’on ne peut voir sous terre…
On en conclut également que l’arc-en-ciel est une vue subjective, et que chacun voit un arc-en-ciel qui lui est propre lorsque le phénomène se produit.
Maintenant, prenons en compte le faît que la lumière blanche comprend toutes les longueurs d’onde visibles pour l’homme ; autrement dit, ne négligeons plus la loi de Cauchy.
Déviation minimale en fonction de l’indice de réfraction de l’eau :
Dm(n)=180+2.arcsin( 
)-4.arcsin(
)
Dérivons cette expression par rapport à n :
= 
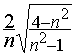
Or, par la loi de Cauchy, l’indice de l’eau est compris entre 1.3 et 1.4 en ce qui concerne les longueurs d’onde étudiées, et, pour ces valeurs de n, cette dérivée existe et est strictement positive. Donc la déviation minimale croit avec l’indice.
De plus, d’après la loi de Cauchy (applicable pour la lumière blanche) :
n=n0+
,et n varie alors, pour l appartenant à [430nm,780nm], de 0.013 . On obtient donc :
n=1.332 pour le rouge, soit Dm=137.78° ;
n=1.345 pour le violet, soit Dm=139.64°.
On obtient finalement un amoncellement (continu) d’arcs de cercle dont chacun a sa propre couleur, car toutes les longeurs d’onde du spectre de la lumière blanche constitue des cônes dont l’angle entre l’axe et les génératrices est à chaque fois différent (et toujours compris entre 40.5° et 42° environ).
C’est cette déviation différente qui entraîne la dispersion des longueurs d’onde, et donc des couleurs.
|
 |
III. L’arc-en-ciel secondaire.
a) Analogies avec l’arc-en-ciel primaire ;
Explication de l’ordre inversé des couleurs.
Il existe d’autres types d’arcs-en-ciel. En effet, ceux-ci présentent souvent un autre arc à l’arc principal, dit primaire. C’est l’arc-en-ciel secondaire.
Les étapes de formation sont pratiquement identiques à l’arc primaire, à ceci près que les rayons subissent non pas une, mais deux réflexions internes dans la goutte d’eau.Les schémas suivants montrent cette différence :
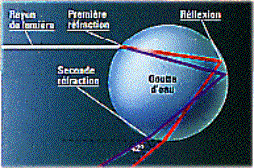
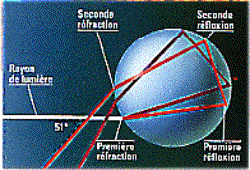
arc « primaire » arc « secondaire »
Le fait qu’il soit moins visible provient de la double réflexion des rayons, ce qui amène plus de perte de lumière. Il est donc plus difficile à observer que l’arc primaire. Autre différence avec ce dernier : on peut remarquer que les couleurs sont inversées. Cela a pour origine la double réflexion des rayons.
Enfin, on remarque que l’arc secondaire paraît être situé au dessus de l’arc primaire : la déviation des rayons n’a pas la même valeur que celle de l’arc étudié auparavant (nous le verrons par la suite).
b) Calcul de la déviation.
Reprenons le calcul de la déviation avec ce nouveau cas de figure : pour cela, on simplifie une fois de plus l’étude en ne s’attachant qu’à un rayon monochromatique.
|
Remarque : b est analogue à la valeur "2.a" de l’arc primaire |
On obtient donc le résultat suivant :
D = 180-b
= 180-(360-2.(180-i)-g)
= 180-360+360+2.i-360+3.(180-2.r)
= 2.i-6.r+360
Et les angles sont en degrés, donc D º D [360] . De plus, on prend la valeur absolue de D.
Ainsi, la déviation s’écrit en fonction de l’angle d’incidence et l’angle du rayon réfracté :
D=6.r-2.i
Or, par la deuxième loi de Snell-Descartes, de même que pour l’arc primaire, on obtient :
r=arcsin(sin(i)/n)
Remarque : étant donné que l’on a pris un rayon monochromatique, n ne varie pas, et on peut donc exprimer la déviation en fonction de l’angle incident i :
D(i)=6.arcsin(sin(i)/n)-2.i
Dérivons l’expression de la déviation pour en chercher les extrema. Là encore, nous étudirons cette fonction sur [0°; 90°] après considération des symétries.
dD=6.dr-2.di
On rappelle le terme dr identique à celui de l’arc primaire :
dr= 
On obtient donc :
= 2.(3. 
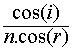-1)
La déviation passe donc par un extremum (qui se révèle être un maximum après étude de la fonction dérivée, strictement positive) pour un certain angle d’incidence, que l’on note im. Cet angle est tel que :
3. 
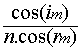-1=0 soit 3.cos(im)=n.cos(rm)
Remarque : pour n fixé à 1.333, on a im » 71.84° , ce qui donne une déviation de 129.1° ou encore une valeur de b égale à 51.9° .
Toujours par le même cheminement que celui effectué dans la deuxième partie, on exprime im en fonction de n :
3.cos(im)=n.cos(rm) soit
3.cos(im)=n.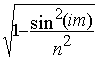 
Û 9.(1-sin2(im))=n2-sin2(im)
Finalement, on trouve:
im=arcsin(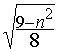 
)
On déduit une nouvelle fois de ces relations une expression reliant la déviation D à l’indice de réfraction de l’eau n :
Dm(n)=6.arcsin(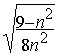 
)-2.arcsin( 
)
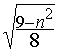L’étude de la dérivée donne :
=- 
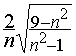
A l’inverse de l’arc primaire, la déviation minimale décroît donc lorsque l’indice de réfraction augmente. Par conséquent, l’angle b diminue lorsque n croît, ce qui implique que l’arc secondaire « violet » sera placé au dessus de l’arc secondaire « rouge ».
|
 |
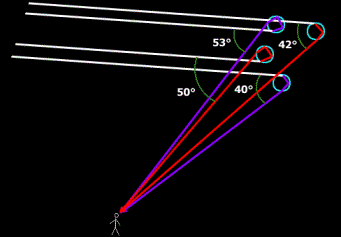Enfin, pour en finir avec les caractéristiques des arcs-en-ciel primaires et secondaires, on peut remarquer expérimentalement qu’il existe un espace sombre entre les deux arcs : c’est ce que l’on nomme la bande sombre d’Alexandre (se référer à la photographie au début du dossier). L’explication de ce phénomène repose sur le faît qu’il n’y a pas de lumière réfléchie pour les angles d’incidence compris entre 42° et 50°, d’où l’aspect sombre de cette bande.
Conclusion.
En définitive, l’arc-en-ciel résulte de deux réfractions différentes selon les longueurs d’onde des couleurs et d’une ou deux réflexion(s) interne(s) pour quelques rayons de lumière avec accumulation suffisante de lumière (selon une certaine déviation) pour laisser une impression à l’œil. C'est un cercle complet dont on ne voit qu'un arc. Ses couleurs proviennent de la superposition des rayons émergeants des innombrables gouttelettes situées aux angles favorables.
De plus, en ce qui concerne l’arc-en-ciel, d’autres théories plus complexes existent, comme par exemple celle de Young et Airy sur les interférences lumineuses qui sont à l’origine des arcs surnuméraires (non abordés dans cet exposé), ou celle de Watson et Poincaré faisant intervenir le moment cinétique des photons dans la goutte.
Enfin, à ce phénomène sont associées de nombreuses légendes: en Europe, un chaudron rempli d’or se trouverait au bout de l’arc-en-ciel, tandis qu’en Afrique, c’est un serpent qui jette le malheur sur la maison qu’il touche…
Voilà, vous êtes maintenant blindés sur la formation de l’arc-en-ciel ! Quelques photos & annexes sont téléchargeables ci-après.
Téléchargement de l’exposé. (fichier .word, 114 Ko. zippé, peu recommandé)
Téléchargement de l'exposé. (fichier .pdf, 185 Ko., recommandé)
Téléchargement d’annexes. (242 Ko. zippé)
Téléchargement de photos. (159 Ko. zippé)
Retour en haut de la page : 
